| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 네카라쿠배당토
- 선형대수학
- 베이지안통계
- 수학적해석학
- recommendation system
- SQL
- 실무로통하는인과추론
- 코세라
- Bayesian
- BigQuery
- 벡터
- 오블완
- 인과추론
- 데이터분석가 코딩테스트
- chatGPT
- 글또10기
- DataAnalyst
- CausalInference
- 데이터 분석
- 인과추론개요
- 티스토리챌린지
- mathematicalthinking
- 나의서양미술순례
- 잠재적결과
- 데이터분석가
- 인과추론 무작위 실험
- 독후감
- 데이터분석
- 빅쿼리
- Recsys
- Today
- Total
Derek 의 데이터 분석 성장기
[실무로 통하는 인과추론] 2장. 무작위 실험과 가설검정 본문

해당 글은 모두 실무로 통하는 인과추론을 기반으로 작성 및 참고하였습니다.
2-1. 무작위 배정으로 독립성 확보
1장에서는 인과관계와 인과추론이 무엇인지에 대해 배웠습니다. 2장에서는 무작위 실험이 인과추론의 가장 중요한 표준이라고 설명합니다. 그 이유는, 1장에서 배웠던 선택편향을 무작위 배정으로 독립성을 확보할 수 있다고 말하고 있습니다.
E[Y | T = 1] - E[Y | T = 0] = E[Y_1 - Y_0 | T=1] + {E[Y_0 | T = 1] - E[Y_0 | T = 0]}
위 공식의 bold는 (ATT + 편향) 으로 표현하고 있습니다.
이 말은, 인과관계와 연관관계가 같기 위해선 두 가지 요소 att + 편향의 합이다 라고 설명하고 있습니다. 따라서 편향이 0 이면 이 둘은 같다라고 말하고 있고요.
그리고, 해당 내용에서는 독립성 가정을 설명하는데요. 독립성 가정은 실험군과 대조군이 비교 가능함을 뜻합니다. 실험군과 대조군의 결과 차이를 유발하는 요인이 바로 Treatment 하나 임을 의미하는 것 이죠. 그리고 RCT(무작위배정)으로 이를 해결할 수 있다고 말하는 것이 해당 장의 내용입니다.
그렇다면 편향을 어떻게 없앨까요?
실험군과 대조군에서 처치 이외의 나머지 조건이 동일(비교) 가능하다면 연관관계는 인과관계가 됩니다. 잠재적 결과가 같다는 말과 동일한데요. 잠재적 결과가 동일하기 위해선 우리가 처치한(Treatment) 효과 이외의 모든 조건이 비슷하거나 같아야 한다는 말과 같습니다.
그리고 이를 가능케 하기 위해선 무작위로 처치를 배정하면 실험군과 대조군의 기댓값은 거의 비교 가능해진다고 합니다. 그리고, 이를 Randomized control trial(RCT) 라고 인과추론에서 부릅니다.
2-2. A/B Test와 신뢰구간
해당 교재에서는 RCT를 보장한 A/B test시 결과를 잘못 해석하지 않기 위해 예재로 설명을 하고 있습니다. (A/B Test 가설검정에 대한 내용입니다.)
예를 들어서, 학교 별로 ENEM(브라질 고등학교 시험) 의 성적을 데이터 예시로 사용합니다. 그리고, 성적이 우수한 학교가 학생수가 적다는 것을 발견했죠,
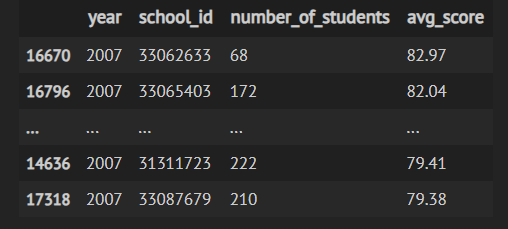
그리고, 상위1%와 아닌 학교의 학생수를 비교하였습니다.

그리고, 규모가 작은 학교일수록 학업 성취도가 작다고 결과를 도출하였다는데요. 그렇지만, 학생수가 적은 학교(표본 크기가 작은 집단)은 샘플 수에 영향을 받기 때문에, 평균의 편차가 굉장히 큽니다. 아래와 같이 분산을 찍어보면 학생수가 적은 학교는 시험 평균 성적이 Middle 에 비해 상대적으로 높거나 낮음의 극단값이 크다는 것을 알 수 있습니다.

그리고, 이는 우리가 알고 싶은 ATE (평균처치효과) 의 값도 신뢰성을 보장하기 어렵다고 말합니다.


이러한 문제를 해결하기 위해선 신뢰구간을 구하고 실제 그룹간의 평균값이 겹치지 않는지. 혹은 신뢰구간이 겹쳐도 통계적으로 유의미한 차이를 보이는지를 확인해야 한다고 합니다.
또한, 신뢰구간 해석의 중요성을 강조하는데요, 어떤 95% 신뢰구간이 95% 확률로 실제 평균을 포함한다고 말해서는 안된다고 말합니다. 특정 신뢰구간은 실제 평균을 포함할 수도, 아닐수도 있다고 합니다. 따라서, 해당 값이 해당 신뢰구간에 포함될 확률이 100%. 그렇지 않은 경우 확률은 0% 라고 합니다. 이는 빈도주의 통계가 모집단 평균을 진정한 모집단 상수로 간주하기 때문이라 하고요.
해당 장에서 하고 싶었던 말은 결국 RCT(무작위 실험) 는 편향을 없애는 올바른 방법이다. 그러나, 제대로 보장되었는지를 확인하기 위해 신뢰구간을 통해 ATE가 우연인지 아닌지 통계적으로 검정하는 것을 의미하고 있습니다.
2-3. 가설검정
2-3 에서는 가설검정을 하는 방법에 대해 얘기합니다.
import seaborn as sns
from matplotlib import pyplot as plt
np.random.seed(123)
n1 = np.random.normal(4, 3, 30000)
n2 = np.random.normal(1, 4, 30000)
n_diff = n2 - n1
plt.figure(figsize=(10,4))
sns.distplot(n1, hist=False, label="$N(4,3^2)$", color="0.0", kde_kws={"linestyle":linestyle[0]})
sns.distplot(n2, hist=False, label="$N(1,4^2)$", color="0.4", kde_kws={"linestyle":linestyle[1]})
sns.distplot(n_diff, hist=False,
label=f"$N(-3, 5^2) = N(1,4^2) - (4,3^2)$", color="0.8", kde_kws={"linestyle":linestyle[1]})
plt.legend();
첫 단계로, 두 분포(그룹)간의 차이를 빼서 새로운 분포를 만드는데요. 이 최종 분포(실선)은 두 분포 평균의 차이이며, 표준편차는 두 분산의 합의 제곱근으로 계산된다고 합니다. 그리고, 실험 결과의 평균 분포에 대해서 설명하기 때문에 이 평균의 표준편차를 평균의 표준오차로 가정합니다.

그리고, 이메일 실험(짧은 이메일(A), 긴 이메일, 이메일 받지 않은 사람간(B)의 전환율)을 분포를 예시로 두 그룹간의 차이로 분포를 구하고, 분포로 평균 차이에 대한 95% 신뢰구간을 구합니다.
diff_mu = short_email.mean() - no_email.mean()
diff_se = np.sqrt(no_email.sem()**2 + short_email.sem()**2)
ci = (diff_mu - 1.96*diff_se, diff_mu + 1.96*diff_se)
print(f"95% CI for the differece (short email - no email):\n{ci}")
x = np.linspace(diff_mu - 4*diff_se, diff_mu + 4*diff_se, 100)
y = stats.norm.pdf(x, diff_mu, diff_se)
plt.figure(figsize=(10,3))
plt.plot(x, y, lw=3)
plt.vlines(ci[1], ymin=0, ymax=4, ls="dotted")
plt.vlines(ci[0], ymin=0, ymax=4, ls="dotted", label="95% CI")
plt.xlabel("Diff. in Conversion (Short - No Email)\n")
plt.legend()
plt.subplots_adjust(bottom=0.15)

그리고 두 그룹간의 전환율 차이는 통계적으로 유의미한지, 아닌지에 대한 분포를 구하는 것이죠.
이것은 결국, 귀무가설 (두 그룹간의 전환율 차이는 없다) 라는 가설을 세우고, 이 신뢰구간은 전환율 차이에 대한 신뢰구간임을 기억해야 합니다. 즉, 귀무가설에 따르면 이 차이는 0 이어야 하지만, 신뢰구간이 0을 완전히 벗어난 것을 우리는 위 분포에서 볼 수 있습니다. 귀무가설이 참이라면 이러한 결과를 관측할 확률이 매우 낮습니다. 따라서 유의수준 a = 0.05(95% 신뢰도) 하에서 귀무가설을 기각 할 수 있습니다.
유의수준(a) : 유의수준 a는 귀무가설이 참인데도 이를 기각하는 1종 오류를 범할 확률을 나타냅니다. 유의수준은 데이터를 수집하거나 분석하기 전에 설정합니다. 위 실험에서는 5%로 설정한 것입니다.
2-3-2. 검정통계량(T-통계량)
신뢰구간 외에도, 때때로 검정 통계량(test statistic)을 사용하여 귀무가설을 기각하기도 합니다. 이는 t-statistic(t-통계량) 이며, 신뢰구간을 형성하는 분포를 정규화함으로서 정의 됩니다. 그리고, 이를 통해 유의수준하에 귀무가설을 기각하는 방법이 있습니다.
# shifting the CI
diff_mu_shifted = short_email.mean() - no_email.mean() - 0.01
diff_se = np.sqrt(no_email.sem()**2 + short_email.sem()**2)
ci = (diff_mu_shifted - 1.96*diff_se, diff_mu_shifted + 1.96*diff_se)
print(f"95% CI 1% difference between (short email - no email):\n{ci}")
t_stat = (diff_mu - 0) / diff_se
t_stat2-4. p 값
앞에서 우리는 이메일을 받지 않은 고객과 짧은 이메일을 받은 고객의 전환율이 동일한데도(=귀무가설) 이렇게 극단적인 차이가 나타날 확률은 5% 미만이라고 했습니다. 하지만, 그 확률을 정확하게 추정할 수 있을지에 대해 의문입니다. 이런 극단적인 값이 관측될 확률이 얼마나 될까요? 이것을 대답할 수 있는 것이 바로 p 값 입니다.
p 값 : p 값은 귀무가설이 참이라고 가정할 때 관측된 결과보다 더 극단적인 결과가 실제로 관측될 확률입니다.
즉, p 값은 귀무가설이 참일 경우 극단적인 데이터가 나타날 확률을 의미합니다.
x = np.linspace(-4, 4, 100)
y = stats.norm.pdf(x, 0, 1)
plt.figure(figsize=(10,4))
plt.plot(x, y, lw=2)
plt.vlines(t_stat, ymin=0, ymax=0.1, ls="dotted", label="T-Stat", lw=2)
plt.fill_between(x.clip(t_stat), 0, y, alpha=0.4, label="P-value")
plt.legend()

p 값은 t-통계량 하에서 귀무가설이 참일 때, 우리가 관측한 두 그룹간의 차이가 관측될 확률값을 보여주고 있습니다. 그리고, 단측 귀무가설(차이가 x보다 크다 or 차이가 x보다 작다) 에서 p 값을 구하려면 표준정규분포표에서 검정통계량 전에 해당하는 영역의 넓이를 계산하면 됩니다. two-sided(양측) 은 귀무가설 차이가 x 이다에서 해당 결과에 2를 곱하면 됩니다.
print("P-value:", (1 - stats.norm.cdf(t_stat))*2)
p 값의 장점 중 하나는 95%나 99% 같은 신뢰수준을 정할필요가 없습니다. 하지만 신뢰수준을 보고하고 싶다면 p 값을 통해 검정이 어느 신뢰수준에서 통과 또는 실패할지 알 수 있습니다. p 값이 0.025인 경우 유의수준이 2.5%인 것과 같습니다.
2-4. 검정력(Power)
우리는 지금까지 a/b Test 실험을 분석하는 법을 배웠습니다. 하지만, 새로운 실험을 설계할 때 몇 명의 고객 이상에게 보내야 귀무가설을 기각하는데 충분한 표본을 수집할까? 이 질문에 대답하기 위해, 충분히 큰 표본을 모집하고 고려해야 합니다.
검정력은 귀무가설을 올바르게 기각할 확률을 말하는 검정력(power of the test)를 의미합니다. 표본이 충분히 커야 통계적 유의미를 가질 수 있습니다.
95% 신뢰구간이란 우리가 실험을 통해 얻은 신뢰구간 중 95%가 추정하고자 하는 매개변수의 실제값을 포함함을 의미합니다. 나머지 5%에서는 실제값을 포함하지 않는데요. 이로인해 5%의 확률로 귀무가설을 잘못 기각하게 됩니다. a(유의수준) 이 0.05일 경우 통계적으로 유의미하다고 결론을 내리기 위해선 매개변수 추정값과 귀무가설 사이의 차이(theta) 최소 0에서 1.96SE 만큼 떨어져 있어야 합니다. 이는 (theta) - 1.96SE가 95% 신뢰구간의 하한이기 때문입니다.
검정력은 올바르게 기각할 확률 1- beta 입니다. 여기서 beta는 귀무가설이 실제로 거짓일 때 이를 기각하지 않을 확률(거짓) 음성이며 이는 일반적으로 기준 80%, 이는 귀무가설이 실제로 거짓일 경우에도 기각하지 않을 확률이 20% 라는 것을 의미합니다.
80%의 검정력을 달성하려면 귀무가설이 거짓일 때 80% 확률로 귀무가설을 기각해야 합니다.
stats.norm.cdf(0.84)
2-5. 표본 크기 계산
그리고, 한가지 더. 실험설계를 하는 입장에서 80%의 검정력과 95%의 신뢰도를 원할 때 표본 크기를 결정하는 공식은 아래와 같습니다.

이는 Minimum detectable effect 이라는 내용을 구글이나 지피티에서 참고하면 좋을 것 같습니다.
2-6. 요약
해당 장에서는 인과추론보다 통계적 검정(신뢰구간, 유의수준, 가설검정)에 대한 이야기가 많았지만 RCT는 결국 두 그룹간의 평균 차이를 검증하기 위한것도 있기 때문에 해당 내용에 집중한 것 같습니다.
인과추정량은 결국 ATE이기 때문이죠. 관측할 수 없는 잠재적 결과인 ATE = E[Y_1 - Y_0] 으로 정의되는 인과추정량입니다. ATE는 독립성 가정(실험군과 대조군의 유일한 차이는 오직 Treatment) 를 통해 식별할 수 있다고 합니다. 혹은 가장 비슷한 두 그룹을 찾아 비교하는 것 입니다.
결국 두 그룹간이 비교가능한 상태라면 두 그룹의 차이로 ate를 구하는 것이고요.
무작위 통제 실험(RCT)을 활용하여 이 가정을 더 타당하게 만드는 방법을 설명하고 있습니다. 처치를 대조군과 실험군에게 무작위로 배정하면 처치와 잠재적 결과 Y_i가 독립이게 만들 수 있다고 말하고 있고요. 그리고, 두 그룹간의 평균차이가 유의미한지를 알기 위해 SE(표준오차), 신뢰구간, 검정력, 표본크기를 계산하여 실험설계하는 법을 설명하는 것이 해당 장의 내용입니다.
* 참고 : 실무로 통화는 인과추론 with Python 교재
* 또한, 개인적으론 인과추론 공부 2회차 입니다! 이번엔 교재를 완독하는 것을 목표로 합니다 :)
'Data > 인과추론' 카테고리의 다른 글
| [실무로 통하는 인과추론] 4. 편향보정 (2) | 2024.11.03 |
|---|---|
| [실무로 통하는 인과추론] 3. 그래프 인과모델 (0) | 2024.10.27 |
| [실무로 통하는 인과추론] 1장 : 인과추론 소개 (4) | 2024.10.09 |
| 3. [인과추론] 무작위 실험(Randomized Control trial) (0) | 2024.02.25 |
| 2. [인과추론] Potential Outcome(잠재적 결과) : What IF? (0) | 2024.02.17 |


